Cosx a formos lygtis. Trigonometrinės lygtys – formulės, sprendiniai, pavyzdžiai. Trupmeninės racionalios trigonometrinės lygtys

Galite užsisakyti išsamų savo problemos sprendimą!!!

Lygybė, turinti nežinomąjį po trigonometrinės funkcijos ženklu („sin x, cos x, tan x“ arba „ctg x“), vadinama trigonometrine lygtimi, todėl toliau nagrinėsime jų formules.

Paprasčiausios lygtys yra „sin x=a, cos x=a, tg x=a, ctg x=a“, kur „x“ yra kampas, kurį reikia rasti, „a“ yra bet koks skaičius. Užrašykime kiekvienos iš jų šaknies formules.

1. Lygtis „sin x=a“.

„|a|>1“ sprendimų nėra.

Kai `|a| \leq 1` turi begalinį sprendinių skaičių.

Šakninė formulė: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Lygtis „cos x=a“.

`|a|>1` – kaip ir sinuso atveju, jis neturi realiųjų skaičių sprendinių.

Kai `|a| \leq 1` turi begalinį sprendinių skaičių.

Šakninė formulė: `x=\pm arccos a + 2\pi n, n \in Z`

Specialūs sinuso ir kosinuso atvejai diagramose.

3. Lygtis „tg x=a“.

Turi begalinį bet kokių „a“ reikšmių sprendimų skaičių.

Šakninė formulė: „x=arctg a + \pi n, n \in Z“.

4. Lygtis „ctg x=a“.

Taip pat turi begalinį bet kokių „a“ reikšmių sprendimų skaičių.

Šakninė formulė: „x=arcctg a + \pi n, n \in Z“.

Lentelėje pateiktų trigonometrinių lygčių šaknų formulės

Dėl sinuso:
Dėl kosinuso:
Tangentui ir kotangentui:
Formulės, skirtos spręsti lygtis, kuriose yra atvirkštinių trigonometrinių funkcijų:

Trigonometrinių lygčių sprendimo būdai

Bet kurios trigonometrinės lygties sprendimas susideda iš dviejų etapų:

paverčiant jį paprasčiausiu;
išspręskite paprasčiausią lygtį, gautą naudodamiesi aukščiau parašytomis šaknies formulėmis ir lentelėmis.

Pažvelkime į pagrindinius sprendimo būdus naudodami pavyzdžius.

Algebrinis metodas.

Šis metodas apima kintamojo pakeitimą ir jo pakeitimą lygybe.

Pavyzdys. Išspręskite lygtį: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0,

pakeiskite: „cos(x+\frac \pi 6)=y“, tada „2y^2-3y+1=0“,

randame šaknis: `y_1=1, y_2=1/2`, iš kurių seka du atvejai:

1. „cos(x+\frac \pi 6)=1“, „x+\frac \pi 6=2\pi n“, „x_1=-\frac \pi 6+2\pi n“.

2. `cos(x+\frac \pi 6)=1/2, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Atsakymas: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Faktorizavimas.

Pavyzdys. Išspręskite lygtį: `sin x+cos x=1`.

Sprendimas. Perkelkime visus lygybės narius į kairę: `sin x+cos x-1=0`. Naudodami , mes transformuojame ir koeficientuojame kairę pusę:

„sin x – 2sin^2 x/2=0“,

„2sin x/2 cos x/2-2sin^2 x/2=0“,

„2sin x/2 (cos x/2-sin x/2) = 0“,

„sin x/2 =0“, „x/2 =\pi n“, „x_1=2\pi n“.
„cos x/2-sin x/2=0“, „tg x/2=1“, „x/2=arctg 1+ \pi n“, „x/2=\pi/4+ \pi n“ , „x_2=\pi/2+ 2\pi n“.

Atsakymas: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Redukcija į homogeninę lygtį

Pirmiausia turite sumažinti šią trigonometrinę lygtį į vieną iš dviejų formų:

"a sin x+b cos x=0" (homogeninė pirmojo laipsnio lygtis) arba "a sin^2 x + b sin x cos x +c cos^2 x=0" (homogeninė antrojo laipsnio lygtis).

Tada padalykite abi dalis iš „cos x \ne 0“ – pirmuoju atveju ir iš „cos^2 x \ne 0“ – antruoju. Gauname „tg x“ lygtis: „a tg x+b=0“ ir „a tg^2 x + b tg x +c =0“, kurias reikia išspręsti žinomais metodais.

Pavyzdys. Išspręskite lygtį: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Sprendimas. Parašykime dešinę pusę kaip „1=sin^2 x+cos^2 x“:

„2 sin^2 x+sin x cos x — cos^2 x=` „sin^2 x+cos^2 x“,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

„sin^2 x+sin x cos x — 2 cos^2 x=0“.

Tai yra vienalytė antrojo laipsnio trigonometrinė lygtis, jos kairę ir dešinę puses padaliname iš `cos^2 x \ne 0`, gauname:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0

„tg^2 x+tg x – 2=0“. Įveskime pakaitalą „tg x=t“, todėl gauname „t^2 + t - 2=0“. Šios lygties šaknys yra „t_1=-2“ ir „t_2=1“. Tada:

„tg x=-2“, „x_1=arctg (-2)+\pi n“, „n \in Z“
„tg x=1“, „x=arctg 1+\pi n“, „x_2=\pi/4+\pi n“, „n \in Z“.

Atsakymas. „x_1=arctg (-2)+\pi n“, „n \in Z“, „x_2=\pi/4+\pi n“, „n \in Z“.

Perėjimas prie pusės kampo

Pavyzdys. Išspręskite lygtį: "11 sin x - 2 cos x = 10".

Sprendimas. Taikykime dvigubo kampo formules ir gausime: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`

„4 tg^2 x/2 – 11 tg x/2 +6=0“.

Taikydami aukščiau aprašytą algebrinį metodą, gauname:

„tg x/2=2“, „x_1=2 arctg 2+2\pi n“, „n \in Z“,
„tg x/2=3/4“, „x_2=arctg 3/4+2\pi n“, „n \in Z“.

Atsakymas. „x_1=2 arctg 2+2\pi n, n \in Z“, „x_2=arctg 3/4+2\pi n“, „n \in Z“.

Pagalbinio kampo įvedimas

Trigonometrinėje lygtyje „a sin x + b cos x =c“, kur a,b,c yra koeficientai, o x yra kintamasis, padalykite abi puses iš „sqrt (a^2+b^2)“:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))".

Kairėje pusėje esantys koeficientai turi sinuso ir kosinuso savybes, būtent jų kvadratų suma lygi 1, o moduliai ne didesni kaip 1. Pažymime juos taip: `\frac a(sqrt (a^2) +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, tada:

`cos \varphi sin x + sin \varphi cos x =C`.

Pažvelkime atidžiau į šį pavyzdį:

Pavyzdys. Išspręskite lygtį: `3 sin x+4 cos x=2`.

Sprendimas. Padalinkite abi lygybės puses iš `sqrt (3^2+4^2)', gausime:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))".

„3/5 sin x+4/5 cos x=2/5“.

Pažymime `3/5 = cos \varphi` , `4/5=sin \varphi`. Kadangi `sin \varphi>0`, `cos \varphi>0`, imame `\varphi=arcsin 4/5` kaip pagalbinį kampą. Tada rašome savo lygybę tokia forma:

„cos \varphi sin x+sin \varphi cos x=2/5“.

Taikydami sinuso kampų sumos formulę, rašome savo lygybę tokia forma:

„sin (x+\varphi)=2/5“,

„x+\varphi=(-1)^n arcsin 2/5+ \pi n“, „n \in Z“,

„x=(-1)^n arcsin 2/5-` „arcsin 4/5+ \pi n“, „n \in Z“.

Atsakymas. „x=(-1)^n arcsin 2/5-` „arcsin 4/5+ \pi n“, „n \in Z“.

Trupmeninės racionalios trigonometrinės lygtys

Tai lygybės su trupmenomis, kurių skaitikliuose ir vardikliuose yra trigonometrinių funkcijų.

Pavyzdys. Išspręskite lygtį. „\frac (sin x)(1+cos x)=1-cos x“.

Sprendimas. Padauginkite ir padalinkite dešinę lygybės pusę iš „(1+cos x)“. Rezultate gauname:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0

„\frac (sin x-sin^2 x)(1+cos x)=0“.

Atsižvelgiant į tai, kad vardiklis negali būti lygus nuliui, gauname `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z.

Prilyginkime trupmenos skaitiklį nuliui: „sin x-sin^2 x=0“, „sin x(1-sin x)=0“. Tada „sin x=0“ arba „1-sin x=0“.

„sin x=0“, „x=\pi n“, „n \in Z“.
„1-sin x=0“, „sin x=-1“, „x=\pi /2+2\pi n, n \in Z“.

Atsižvelgiant į tai, kad ` x \ne \pi+2\pi n, n \in Z, sprendiniai yra `x=2\pi n, n \in Z` ir `x=\pi /2+2\pi n` , „n \in Z“.

Atsakymas. „x=2\pi n“, „n \in Z“, „x=\pi /2+2\pi n“, „n \in Z“.

Trigonometrija, o ypač trigonometrinės lygtys, naudojamos beveik visose geometrijos, fizikos ir inžinerijos srityse. Mokytis pradedama 10 klasėje, vieningam valstybiniam egzaminui visada yra užduočių, tad pasistenkite atsiminti visas trigonometrinių lygčių formules – jos jums tikrai pravers!

Tačiau net nereikia jų įsiminti, svarbiausia suprasti esmę ir mokėti ją išvesti. Tai nėra taip sunku, kaip atrodo. Įsitikinkite patys žiūrėdami vaizdo įrašą.

Paprasčiausios trigonometrinės lygtys paprastai išsprendžiamos naudojant formules. Leiskite jums priminti, kad paprasčiausios trigonometrinės lygtys yra šios:

sinx = a

cosx = a

tgx = a

ctgx = a

x yra kampas, kurį reikia rasti,
a yra bet koks skaičius.

O štai formulės, kuriomis iš karto galite užrašyti šių paprasčiausių lygčių sprendinius.

Dėl sinuso:

Dėl kosinuso:

x = ± arccos a + 2π n, n ∈ Z

Dėl liestinės:

x = arctan a + π n, n ∈ Z

Dėl kotangento:

x = arcctg a + π n, n ∈ Z

Tiesą sakant, tai yra teorinė paprasčiausių trigonometrinių lygčių sprendimo dalis. Be to, viskas!) Visai nieko. Tačiau klaidų skaičius šioje temoje tiesiog nepastebimas. Ypač jei pavyzdys šiek tiek skiriasi nuo šablono. Kodėl?

Taip, nes daug žmonių rašo šias raides, visai nesuprasdami jų prasmės! Jis rašo atsargiai, kad kas nors neatsitiktų...) Tai reikia sutvarkyti. Trigonometrija žmonėms arba žmonės trigonometrijai!?)

Išsiaiškinkime?

Vienas kampas bus lygus arccos a, antra: -arccos a.

Ir visada taip pavyks. Bet kuriam A.

Jei netikite manimi, užveskite pelės žymeklį ant nuotraukos arba palieskite paveikslėlį planšetiniame kompiuteryje.) Pakeičiau numerį. A į kažką neigiamo. Šiaip ar taip, gavome vieną kampą arccos a, antra: -arccos a.

Todėl atsakymą visada galima parašyti kaip dvi šaknų serijas:

x 1 = arccos a + 2π n, n ∈ Z

x 2 = - arccos a + 2π n, n ∈ Z

Sujungkime šias dvi serijas į vieną:

x= ± arccos a + 2π n, n ∈ Z

Ir viskas. Gavome bendrą formulę, kaip išspręsti paprasčiausią trigonometrinę lygtį su kosinusu.

Jei supranti, kad tai ne kažkokia supermokslinė išmintis, bet tik sutrumpinta dviejų atsakymų serijų versija, Taip pat galėsite atlikti užduotis „C“. Su nelygybėmis, su šaknų parinkimu iš duoto intervalo... Ten atsakymas su pliusu/minusu neveikia. Bet jei atsakymą traktuosite dalykiškai ir suskirstysite jį į du atskirus atsakymus, viskas išsispręs.) Tiesą sakant, todėl mes tai ir nagrinėjame. Kas, kaip ir kur.

Paprasčiausioje trigonometrinėje lygtyje

sinx = a

taip pat gauname dvi šaknų serijas. Visada. Ir šias dvi serijas taip pat galima įrašyti vienoje eilutėje. Tik ši eilutė bus sudėtingesnė:

x = (-1) n arcsin a + π n, n ∈ Z

Tačiau esmė išlieka ta pati. Matematikai paprasčiausiai sukūrė formulę, kad šaknų serijoms būtų įvestas vienas, o ne du. Tai viskas!

Patikrinkime matematikus? Ir niekada nežinai...)

Ankstesnėje pamokoje buvo išsamiai aptartas trigonometrinės lygties su sinusu sprendimas (be formulių):

Atsakymas lėmė dvi šaknų serijas:

x 1 = π /6 + 2π n, n ∈ Z

x 2 = 5π /6 + 2π n, n ∈ Z

Jei tą pačią lygtį išspręsime naudodami formulę, gausime atsakymą:

x = (-1) n arcsin 0,5 + π n, n ∈ Z

Tiesą sakant, tai nebaigtas atsakymas.) Mokinys turi tai žinoti arcsin 0,5 = π /6. Pilnas atsakymas būtų toks:

x = (-1) n π /6+ π n, n ∈ Z

Tai kelia įdomų klausimą. Atsakyti per x 1; x 2 (tai teisingas atsakymas!) ir per vienišius X (ir tai teisingas atsakymas!) – ar tai tas pats dalykas, ar ne? Dabar išsiaiškinsime.)

Atsakyme pakeičiame su x 1 vertybes n =0; 1; 2; ir tt, suskaičiuojame, gauname šaknų seriją:

x 1 = π/6; 13π/6; 25π/6 ir taip toliau.

Su tuo pačiu pakeitimu atsakant su x 2 , mes gauname:

x 2 = 5π/6; 17π/6; 29π/6 ir taip toliau.

Dabar pakeiskime reikšmes n (0; 1; 2; 3; 4...) į bendrą viengubo formulę X . Tai yra, minus vieną padidiname iki nulinės galios, tada į pirmą, antrą ir tt. Na, žinoma, mes pakeičiame 0 į antrąjį terminą; 1; 2 3; 4 ir kt. Ir skaičiuojame. Gauname seriją:

x = π/6; 5π/6; 13π/6; 17π/6; 25π/6 ir taip toliau.

Tai viskas, ką matote.) Bendroji formulė mums pateikia lygiai tokie patys rezultatai kaip ir du atsakymai atskirai. Tiesiog viskas iš karto, tvarkinga. Matematikai nebuvo apgauti.)

Taip pat galima patikrinti trigonometrinių lygčių su liestine ir kotangentu sprendimo formules. Bet mes to nedarysime.) Jie jau paprasti.

Visą šį pakeitimą ir tikrinimą parašiau specialiai. Čia svarbu suprasti vieną paprastą dalyką: yra elementariųjų trigonometrinių lygčių sprendimo formulės, tik trumpa atsakymų santrauka. Dėl šio trumpumo į kosinuso tirpalą turėjome įterpti pliusą / minusą ir (-1) n į sinuso tirpalą.

Šie intarpai jokiu būdu netrukdo atlikti užduotis, kur tereikia užrašyti elementarios lygties atsakymą. Bet jei jums reikia išspręsti nelygybę arba jums reikia ką nors padaryti su atsakymu: pasirinkti šaknis intervale, patikrinti, ar nėra ODZ ir pan., šie įterpimai gali lengvai nuliūdinti žmogų.

Taigi ką turėčiau daryti? Taip, arba parašykite atsakymą dviem eilėmis, arba išspręskite lygtį/nelygybę naudodami trigonometrinį apskritimą. Tada šie intarpai išnyksta ir gyvenimas tampa lengvesnis.)

Galime apibendrinti.

Norint išspręsti paprasčiausias trigonometrines lygtis, yra paruoštos atsakymų formulės. Keturi gabaliukai. Jie tinkami norint iš karto užrašyti lygties sprendimą. Pavyzdžiui, jums reikia išspręsti lygtis:

sinx = 0,3

Lengvai: x = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Jokiu problemu: x = ± lankai 0,2 + 2π n, n ∈ Z

tgx = 1,2

Lengvai: x = arctan 1,2 + π n, n ∈ Z

ctgx = 3,7

Liko vienas: x= arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Jeigu tu, spindėdamas žiniomis, iškart parašyk atsakymą:

x= ± lankai 1,8 + 2π n, n ∈ Z

tada jau šviečiate, tai... tai... iš balos.) Teisingas atsakymas: sprendimų nėra. Nesuprantu kodėl? Perskaitykite, kas yra lanko kosinusas. Be to, jei dešinėje pradinės lygties pusėje yra sinuso, kosinuso, liestinės, kotangento lentelės vertės, - 1; 0; √3; 1/2; √3/2 ir taip toliau. - atsakymas per arkas bus nebaigtas. Arkos turi būti paverstos radianais.

Ir jei susidursite su nelygybe, pvz

tada atsakymas yra:

x πn, n ∈ Z

yra reta nesąmonė, taip...) Čia reikia išspręsti naudojant trigonometrinį apskritimą. Ką mes darysime atitinkamoje temoje.

Tiems, kurie herojiškai skaito šias eilutes. Aš tiesiog negaliu neįvertinti jūsų titaniškų pastangų. Premija jums.)

Premija:

Rašydami formules nerimą keliančioje kovos situacijoje, net patyrę vėplai dažnai susipainioja, kur πn, Ir kur 2π n. Štai jums paprastas triukas. Į Visi formulės vertos πn. Išskyrus vienintelę formulę su lanko kosinusu. Ten stovi 2πn. Du peen. raktinis žodis – du. Toje pačioje formulėje yra du pradžioje. Pliusas ir minusas. Čia ir ten - du.

Taigi, jei parašėte duženklą prieš lanko kosinusą, lengviau atsiminti, kas atsitiks pabaigoje du peen. Ir tai atsitinka ir atvirkščiai. Žmogus praleis ženklą ± , pasiekia pabaigą, rašo taisyklingai du Pienas, ir jis susipras. Kažkas laukia du pasirašyti! Žmogus grįš į pradžią ir ištaisys klaidą! Kaip šitas.)

Jei jums patinka ši svetainė...

Beje, turiu jums dar keletą įdomių svetainių.)

Galite praktikuotis spręsdami pavyzdžius ir sužinoti savo lygį. Testavimas su momentiniu patvirtinimu. Mokykimės – su susidomėjimu!)

Galite susipažinti su funkcijomis ir išvestinėmis.

Centruota taške A.
α - kampas, išreikštas radianais.

Apibrėžimas
Sinusas (sin α) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi priešingos kojos ilgio santykiui |BC| iki hipotenuzės ilgio |AC|.

Kosinusas (cos α) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi gretimos kojos ilgio santykiui |AB| iki hipotenuzės ilgio |AC|.

Priimti užrašai

;
;
.

Sinuso funkcijos grafikas, y = sin x

Kosinuso funkcijos grafikas, y = cos x

Sinuso ir kosinuso savybės

Periodiškumas

Funkcijos y = nuodėmė x ir y = cos x periodinis su periodu 2π.

Paritetas

Sinuso funkcija yra nelyginė. Kosinuso funkcija yra lygi.

Apibrėžimo ir vertybių sritis, ekstremumai, padidėjimas, sumažėjimas

Sinuso ir kosinuso funkcijos yra tolydžios savo apibrėžimo srityje, ty visiems x (žr. tęstinumo įrodymą). Pagrindinės jų savybės pateiktos lentelėje (n – sveikas skaičius).

	y = nuodėmė x	y = cos x
Taikymo sritis ir tęstinumas	- ∞ < x < + ∞	- ∞ < x < + ∞
Vertybių diapazonas	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Didėja
Mažėjantis
Maxima, y = 1
Minimalus, y = - 1
Nuliai, y = 0
Sukirtimo taškai su ordinačių ašimi, x = 0	y = 0	y = 1

Pagrindinės formulės

Sinuso ir kosinuso kvadratų suma

Sinuso ir kosinuso formulės iš sumos ir skirtumo

;
;

Sinusų ir kosinusų sandaugos formulės

Sumos ir skirtumo formulės

Sinuso išreiškimas per kosinusą

;
;
;
.

Kosinuso išreiškimas per sinusą

;
;
;
.

Išraiška per tangentą

; .

Kada turime:
; .

adresu:
; .

Sinusų ir kosinusų, liestinių ir kotangentų lentelė

Šioje lentelėje parodytos sinusų ir kosinusų reikšmės tam tikroms argumento reikšmėms.

Išraiškos per sudėtingus kintamuosius

;

Eulerio formulė

Išraiškos per hiperbolines funkcijas

;
;

Dariniai

; . Išvestinės formulės >>>

N-osios eilės vediniai:
{ -∞ < x < +∞ }

Sekantas, kosekantas

Atvirkštinės funkcijos

Atvirkštinės sinuso ir kosinuso funkcijos yra atitinkamai arcsinusas ir arkosinusas.

Arčinas, arcsin

Arkosinas, arkosas

Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir kolegijų studentams, „Lan“, 2009 m.

Zacharova Liudmila Vladimirovna
Barnaulo MBOU „Vidurinė mokykla Nr. 59“.
matematikos mokytojas [apsaugotas el. paštas]

№1 Paprasčiausios trigonometrinės lygtys

Tikslas: 1. Išveskite paprasčiausių formos trigonometrinių lygčių sprendinių formules sinx =a, cosx=a, tgx=a, ctgx=a;

2. Išmokti spręsti paprastas trigonometrines lygtis naudojant formules.

Įranga: 1) Lentelės su trigonometrinių funkcijų grafikais y= sinx, y=cosx, y=tgx, y=ctgx; 2) Atvirkštinių trigonometrinių funkcijų verčių lentelė; 3) Paprastų trigonometrinių lygčių sprendimo formulių suvestinė.

Paskaitos pamokos planas:

1 .Lygties šaknų formulių išvedimas

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Žodinis frontalinis darbas gautoms formulėms konsoliduoti.

3 . Rašto darbas studijuotai medžiagai įtvirtinti

Per užsiėmimus.

Algebroje, geometrijoje, fizikoje ir kituose dalykuose susiduriame su įvairiomis problemomis, kurias sprendžiant reikia spręsti lygtis. Mes ištyrėme trigonometrinių funkcijų savybes, todėl natūralu kreiptis į lygtis, kuriose nežinomasis yra po funkcijos ženklu

Apibrėžimas: Formos lygtys sinx = a , cosx= a , tgx= a , ctgx= A vadinamos paprasčiausiomis trigonometrinėmis lygtimis.

Labai svarbu išmokti išspręsti paprasčiausias trigonometrines lygtis, nes visi bet kokių trigonometrinių lygčių sprendimo būdai ir būdai susideda iš jų sumažinimo iki paprasčiausių.

Pradėkime nuo formulių, kurios „aktyviai“ veikia sprendžiant trigonometrines lygtis.

1.Sinx = formos lygtys a.

Išspręskime lygtį sinx = a grafiškai. Norėdami tai padaryti, vienoje koordinačių sistemoje sudarysime funkcijų y=sinx ir y= grafikus A.

1) Jei A> 1 ir A nuodėmė x= A neturi sprendinių, nes tiesė ir sinusinė banga neturi bendrų taškų.

2) Jei -1a a sinusinę bangą kerta be galo daug kartų. Tai reiškia, kad lygtis sinx= a turi be galo daug sprendimų.

Kadangi sinuso periodas yra 2 , tada išspręsti lygtį sinx= a pakanka rasti visus sprendimus bet kuriame 2 ilgio segmente.

Lygties sprendimas [-/2; /2] pagal arcsinuso apibrėžimą x= arcsin a, o ant x=-arcsin a. Atsižvelgdami į funkcijos у=sinx periodiškumą, gauname tokias išraiškas

x = -arcsin a+2n, n Z.

Abi sprendimų serijos gali būti derinamos

X = (-1) n arcsin a+n, nZ.

Šiais trimis atvejais jie nori naudoti paprastesnius ryšius, o ne bendrą formulę:

Jeigu A=-1, tada sin x =-1, x=-/2+2n

Jeigu A=1, tada sin x =1, x =/2+2n

Jeigu a= 0, tada sin x =0. x = n,

Pavyzdys: išspręskite lygtį sinx = 1/2.

Sukurkime sprendimų formules x = lankas 1/2+ 2n

X= - arcsin a+2n

Apskaičiuokime vertę arcsin1/2. Rastą reikšmę pakeiskime sprendinių formulėmis

x=5/6+2n

arba pagal bendrąją formulę

X = (-1) n arcsin 1/2+n,

X= (-1) n /6+n,

2. Formos lygtys cosx= a.

Išspręskime lygtį cosx= a taip pat grafiškai, nubraižant funkcijas y= cosx ir y= A.

1) Jei 1, tai lygtis cosx= a neturi sprendinių, nes grafikai neturi bendrų taškų.

2) Jei -1 a cosx= a turi begalę sprendimų.

Rasime visus sprendimus cosx= a 2 ilgio intervale, nes kosinuso periodas yra 2.

Pagal lankinio kosinuso apibrėžimą lygties sprendimas bus x= arcos a. Atsižvelgiant į kosinuso funkcijos paritetą, lygties [-;0] sprendimas bus x=-arcos a.

Taigi, sprendžiant lygtį cosx= a x= + arcos a+ 2 n,

Trimis atvejais naudosime ne bendrąją formulę, o paprastesnius ryšius:

Jeigu A=-1, tada cosx =-1, x =-/2+2n

Jeigu A=1, tada cosx =1, x = 2n,

Jei a=0, tai cosx=0. x =/2+n

Pavyzdys: išspręskite lygtį cos x = 1/2,

Sukurkime sprendimų formules x=arccos 1/2+ 2n

Apskaičiuokime vertę arccos1/2.

Rastą reikšmę pakeiskime sprendinių formulėmis

X= + /3+ 2n, nZ.

Formos lygtys tgx= a.

Kadangi liestinės periodas yra lygus, tada norint rasti visus lygties sprendinius tgx= a, pakanka rasti visus sprendimus bet kuriame ilgio intervale. Pagal arctangento apibrėžimą lygties (-/2; /2) sprendimas yra arctanas a. Atsižvelgiant į funkcijos laikotarpį, visi lygties sprendiniai gali būti parašyti forma

x = arctan a+ n, nZ.

Pavyzdys: Išspręskite lygtįįdegis x = 3/3

Sukurkime formulę x= sprendimui arctan 3/3 +n, nZ.

Apskaičiuokime arctangento reikšmę arctan 3/3= /6, tada

X=/6+ n, nZ.

Lygties sprendimo formulės išvedimas Su tgx= a gali būti teikiama studentams.

Pavyzdys.

Išspręskite lygtį ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

Išstudijavę medžiagą, studentai gali užpildyti lentelę:

„Trigonometrinių lygčių sprendimas“.

lygtis

Pratimai studijuojamai medžiagai įtvirtinti.

(Žodžiu) Kurią iš parašytų lygčių galima išspręsti naudojant formules:

a) x= (-1) n arcsin a+n, nZ;

b) x= + arcos a+ 2 n?

cos x = 2/2, tan x = 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 .

Kurios iš šių lygčių neturi sprendinių?

Išspręskite lygtis:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) įdegis x = 3; g) vaikiška lovelė x = -1; j) įdegis x = 1/3.

3. Išspręskite lygtis:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 = 1/2; e) 3 tg 3x =1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

Sprendžiant šias lygtis, pravartu užsirašyti formos lygčių sprendimo taisykles nuodėmė V x = a, Ir Su nuodėmė V x = a, | a|1.

Nuodėmė V x = a, |a|1.

V x = (-1) n arcsin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Apibendrinant pamoką:

Šiandien klasėje išvedėme paprastų trigonometrinių lygčių sprendimo formules.

Mes pažvelgėme į paprastų trigonometrinių lygčių sprendimo pavyzdžius.

Užpildėme lentelę, kurią naudosime spręsdami lygtis.

Namų darbai.

№2 Trigonometrinių lygčių sprendimas

Tikslas: Trigonometrinių lygčių sprendimo tyrimo metodai: 1) redukuojamosios į kvadratines 2) redukuojamos į vienarūšes trigonometrines lygtis.

Ugdyti mokinių stebėjimo gebėjimus taikant įvairius trigonometrinių lygčių sprendimo būdus.

Frontalinis darbas su studentais.

Kokios yra trigonometrinių lygčių šaknų formulės? cos x= a, sin x= a, tgx = a, ctg x = a.

Išspręskite lygtis (žodžiu):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Raskite klaidas ir pagalvokite apie klaidų priežastis.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Naujos medžiagos studijavimas.

Ši pamoka apims kai kuriuos dažniausiai naudojamus trigonometrinių lygčių sprendimo būdus.

Trigonometrinės lygtys sumažintos iki kvadratinės.

Į šią klasę gali būti įtrauktos lygtys, apimančios vieną funkciją (sinusą arba kosinusą) arba dvi to paties argumento funkcijas, tačiau viena iš jų sumažinama iki antrosios naudojant pagrindines trigonometrines tapatybes.

Pvz., jei cosх į lygtį įveda lygiais laipsniais, tai ją pakeičiame 1-sin 2 x, jei sin 2 x, tai pakeičiame 1-cos 2 x.

Pavyzdys.

Išspręskite lygtį: 8 sin 2 x - 6sin x -5 =0.

Sprendimas: pažymėkime sin x=t, tada 8t 2 – 6t – 5=0,

D = 196,

T 1 = -1/2, t 2 = -5/4.

Atlikime atvirkštinį pakeitimą ir išspręskime šias lygtis.

X=(-1) k+1 /6+ k, kZ.

Nuo -5/4>1 lygtis neturi šaknų.

Atsakymas: x=(-1) k+1 /6+ k, kZ.

Konsolidavimo pratimų sprendimas.

Išspręskite lygtį:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

Homogeninės trigonometrinės lygtys.

Apibrėžimas: 1) Formos lygtisa sinx + b cosx=0, (a=0, b=0) vadinama homogenine pirmojo laipsnio lygtimi sin x ir cos x atžvilgiu.

Ši lygtis išspręsta padalijus abi puses iš cosx 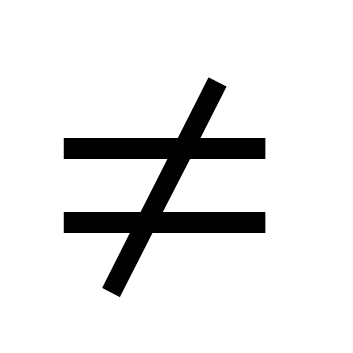0. Rezultatas yra lygtis atgx+ b=0.

2) Formos lygtisa nuodėmė 2 x + b sinx cosx + c cos 2 x =0 vadinama homogenine antrojo laipsnio lygtimi, kur a, b, c yra bet kokie skaičiai.

Jei a = 0, tai lygtį išspręsime padalydami abi puses iš cos 2x 0. Rezultate gauname lygtį atg 2 x+ btgx+с =0.

komentaras: Formos lygtisa nuodėmė mx + b cos mx=0 arba

a nuodėmė 2 mx + b nuodėmė mx cos mx + c cos 2 mx =0 taip pat yra vienalytės. Norėdami juos išspręsti, abi lygties pusės yra padalintos iš cos mx=0 arba cos 2 mx=0

3) Įvairios lygtys, kurios iš pradžių nėra vienalytės lygtys, gali būti redukuojamos į vienarūšes lygtis. Pavyzdžiui,nuodėmė 2 mx + b nuodėmė mx cos mx + c cos 2 mx = d, Ir a sinx + b cosx= d. Norėdami išspręsti šias lygtis, turite padauginti dešinę pusę iš "trigonometrinis vienetas" tie. įjungta nuodėmė 2 x + cos 2 x ir atlikti matematines transformacijas.

Pratimai išmoktai medžiagai įtvirtinti:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Pamokos apibendrinimas. Namų darbai.

Šioje pamokoje, priklausomai nuo grupės pasirengimo, galite apsvarstyti formos lygčių sprendimą a sin mx +b cos mx=c, kur a, b, c tuo pačiu metu nėra lygūs nuliui.

Stiprinimo pratimai:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Trigonometrinių lygčių sprendimas

Tikslas: 1) Išstudijuoti trigonometrinių lygčių sprendimo faktoriais metodą; išmokti spręsti trigonometrines lygtis naudojant įvairias trigonometrines formules;

2) Patikrinkite: mokinių žinias apie paprastų trigonometrinių lygčių sprendimo formules; gebėjimas spręsti paprastas trigonometrines lygtis.

Pamokos planas:

Namų darbų tikrinimas.

Matematinis diktantas.

Naujos medžiagos mokymasis.

Savarankiškas darbas.

Apibendrinant pamoką. Namų darbai.

Pamokos eiga:

Namų darbų tikrinimas (lentoje trumpai užrašomi trigonometrinių lygčių sprendiniai).

Matematinis diktantas.

1. Kokios lygtys vadinamos paprasčiausiomis trigonometrinėmis lygtimis?

2. Kaip vadinasi formos lygtisa sinx + b cosx=0? Nurodykite būdą, kaip ją išspręsti.

3.Užrašykite lygties šaknų formulę tgx = a(ctg x= a).

4. Užrašykite formos lygčių šaknų formules cosx= a, Kur A=1, A=0, A=-1.

5. Užrašykite bendrąją lygties šaknų formulę nuodėmė x= a, | a|

6. Kaip sprendžiamos formos lygtysa cosx= b, | b|

AT 2

1. Užrašykite lygčių šaknų formules cosx= a,| a|

2. Užrašykite bendrąją lygties šaknų formulę

= a, | a|

3. Kaip vadinamos formos lygtys? nuodėmė x= a, tgx = a, nuodėmė x= a?

4.Užrašykite lygties šaknų formules nuodėmė x= a, Jeigu A=1, A=0, A=-1.

5. Kaip sprendžiamos formos lygtys nuodėmė a x= b, | b|

6. Kokios lygtys vadinamos antrojo laipsnio vienarūšėmis lygtimis? Kaip jie išsprendžiami?

Naujos medžiagos mokymasis.

Faktorizacijos metodas.

Vienas iš dažniausiai naudojamų trigonometrinių lygčių sprendimo būdų yra faktorizavimo metodas.

Jei lygtis f(x) =0 gali būti pavaizduota kaip f 1 (x) f 2 (x) =0, tada uždavinys redukuojamas į dviejų lygčių f 1 (x) = 0, f 2 (x) = 0 sprendimą. .

(Su mokiniais naudinga prisiminti taisyklę “ Veiksnių sandauga yra lygi nuliui, jei bent vienas iš veiksnių yra lygus nuliui, o kiti turi prasmę»)

Tirtos medžiagos konsolidavimas sprendžiant įvairaus sudėtingumo lygtis.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(savaime)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 būdai)

7) cosx+ cos3x=0; 8) sin 3x= nuodėmė 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0 (savaime)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Savarankiškas darbas.

1 variantas 2 variantas

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Pamokos apibendrinimas. Namų darbai.

Žinome, kad kosinuso reikšmės yra [-1; 1], t.y. -1 ≤ cos α ≤ 1. Todėl jei |a| > 1, tada lygtis cos x = a šaknų neturi. Pavyzdžiui, lygtis cos x = -1,5 neturi šaknų.

Panagrinėkime keletą problemų.

Išspręskite lygtį cos x = 1/2.

Sprendimas.

Prisiminkite, kad cos x yra apskritimo, kurio spindulys lygus 1, taško abscisė, gauta pasukus tašką P (1; 0) kampu x aplink pradžios tašką.

Abscisė 1/2 yra dviejuose apskritimo taškuose M 1 ir M 2. Kadangi 1/2 = cos π/3, tai tašką M 1 galime gauti iš taško P (1; 0) sukdami kampu x 1 = π/3, taip pat kampais x = π/3 + 2πk, kur k = +/-1, +/-2, …

Taškas M 2 gaunamas iš taško P (1; 0) sukant kampu x 2 = -π/3, taip pat kampais -π/3 + 2πk, kur k = +/-1, +/-2 ,...

Taigi visas lygties cos x = 1/2 šaknis galima rasti naudojant formules
x = π/3 + 2πk
x = -π/3 + 2πk,

Dvi pateiktos formulės gali būti sujungtos į vieną:

x = +/-π/3 + 2πk, k € Z.

Išspręskite lygtį cos x = -1/2.

Sprendimas.

Dviejų apskritimo taškų M 1 ir M 2 abscisė lygi – 1/2. Kadangi -1/2 = cos 2π/3, tai kampas x 1 = 2π/3, taigi kampas x 2 = -2π/3.

Vadinasi, visas lygties cos x = -1/2 šaknis galima rasti naudojant formulę: x = +/-2π/3 + 2πk, k € Z.

Taigi kiekviena iš lygčių cos x = 1/2 ir cos x = -1/2 turi begalinį šaknų skaičių. Intervale 0 ≤ x ≤ π kiekviena iš šių lygčių turi tik vieną šaknį: x 1 = π/3 yra lygties cos šaknis x = 1/2, o x 1 = 2π/3 yra lygties cos šaknis. x = -1/2.

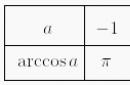
Skaičius π/3 vadinamas skaičiaus 1/2 arkosinusu ir rašomas: arccos 1/2 = π/3, o skaičius 2π/3 vadinamas skaičiaus (-1/2) arkosinusu ir parašytas : arccos (-1/2) = 2π/3 .

Apskritai lygtis cos x = a, kur -1 ≤ a ≤ 1, intervale 0 ≤ x ≤ π turi tik vieną šaknį. Jei a ≥ 0, tada šaknis yra intervale ; jeigu< 0, то в промежутке (π/2; π]. Этот корень называют арккосинусом числа а и обозначают: arccos а.

Taigi skaičiaus a lankinis kosinusas € [-1; 1 ] yra skaičius a €, kurio kosinusas yra lygus a:

arccos а = α, jei cos α = а ir 0 ≤ а ≤ π (1).

Pavyzdžiui, arkos √3/2 = π/6, nes cos π/6 = √3/2 ir 0 ≤ π/6 ≤ π;
arckos (-√3/2) = 5π/6, nes cos 5π/6 = -√3/2 ir 0 ≤ 5π/6 ≤ π.

Lygiai taip pat, kaip buvo padaryta sprendžiant 1 ir 2 uždavinius, galima parodyti, kad visos lygties šaknys cos x = a, kur |a| ≤ 1, išreikštas formule

x = +/-arccos a + 2 πn, n € Z (2).

Išspręskite lygtį cos x = -0,75.

Sprendimas.

Naudodami (2) formulę randame x = +/-arccos (-0,75) + 2 πn, n € Z.

Arkos reikšmę (-0,75) galima apytiksliai rasti paveikslėlyje, matuojant kampą naudojant transporterį. Apytiksles lanko kosinuso reikšmes taip pat galima rasti naudojant specialias lenteles (Bradis lenteles) arba mikroskaičiuotuvą. Pavyzdžiui, arccos reikšmę (-0,75) galima apskaičiuoti naudojant mikroskaičiuotuvą ir gauti apytikslę reikšmę 2,4188583. Taigi, arkos (-0,75) ≈ 2,42. Todėl arkos (-0,75) ≈ 139°.

Atsakymas: arkos (-0,75) ≈ 139°.